The Archive contains a complete collection of Hero Cards. These artistic masterpieces display the strengths and weaknesses of all heroes from all realities by assigning them numbers for different attributes. Although there is a certain satisfaction in finally ascertaining who would win in a fight between warriors from incompatible universes, you cannot help but wonder if this tiny set of numbers is really sufficient to accurately portray their power.
If you want your players to make D&D 5e characters, step 3 is to Determine Ability Scores. However, I will defy the decree of the Wizards of the Coast, and address it first. Why? The short answer is that it is easier. Steps 1 and 2 are about Race and Class. We will examine how and why, as DMs, we can make changes to that part of character creation, but it will require at least one academic study and several thousand character sheets. For now, we will ease our way in with Ability Scores.
Ability Score generation is also one of the first places where DMs start doing things differently. Do you roll, use an array, or do point buy? In order, or roll and assign? What do you roll, or how many points do you spend? There are lots of options to compare, so it is a good opportunity to practice making these kinds of comparison.
This article will focus on 5e. Most d20 systems should be similar. Other systems with ability scores may not use these methods, but perhaps the analysis will help inform those decisions.
Dream Ability Scores
Characters have six ability scores. These scores cannot normally increase past 20, and the Ability Scores and Modifiers table in the PHB would suggest that under no circumstances can they increase past 30, or below 1. Finally, the suggested methods for generating scores mean they are always between 3 and 18, and normally between 8 and 15.
From this RPGBOT analysis, we can see the importance of having at least 16 in one’s primary ability score. Although the table focuses on attack rolls, the maths also applies to a caster’s save DC. 5e characters are generally not MAD (multi-ability score dependent), so rarely rely on having two high primary ability scores. However, all characters need to not get hit and have hitpoints. This makes Constitution essential (despite it not being a primary ability score for any class), and Dexterity good for anyone without heavy armour. If your class does not need them, Charisma and Strength are generally irrelevant, and Wisdom and Intelligence are needed only for skills and saves.
Based on the above, the ideal set ability scores (ignoring all at maximum) would include a 16, two 14s, and some low values we are less bothered about. Without this, the character will not function as effectively as the game intends. This is not necessarily an issue, but can be a source of frustration, especially if it leads to other PCs overshadowing them.
My final point about dream ability scores is more ideological. Some people like to control their ability scores in order to sculpt their character into their desired build. Some people want to inject randomness to spare themselves the maths-heavy analysis. Still others do not care about this at all, and just want something that works. If your group leans heavily one way, do that! Ultimately, this is a game, and is about having fun. My preference is for something that gets the best of all worlds: a simple system with a degree of randomness that still lets players shape their builds the way they want.
Ability Scores by the Book
The PHB offers three ways of generating ability scores: 4d6, drop low; the standard array; and point buy.
4d6 Drop Lowest
This is perhaps the most well-known method. Each score is generated by rolling 4d6 and summing the highest three. After generating size scores, the player assigns them to the abilities of their choice. As all ability scores are generated independently of one another and by the same method, they will all be random values drawn from the same distribution.
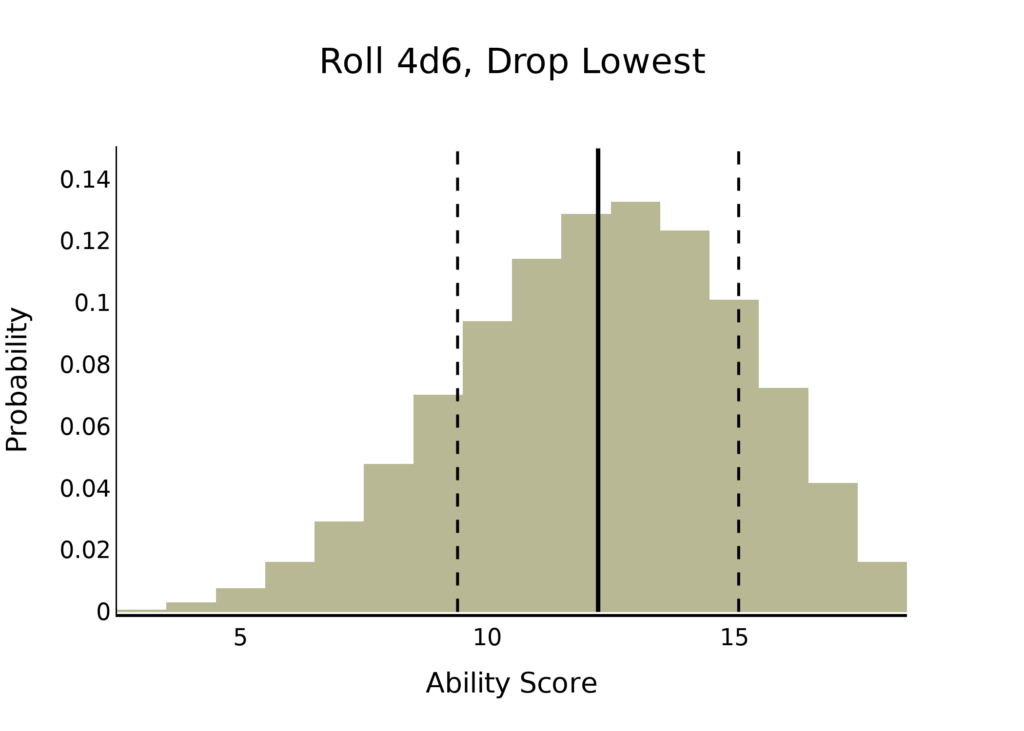
This figure shows the probability of rolling each ability score. The solid line is the mean, and tells us that an average roll will generate an ability score of 12.3. The dashed line indicate one standard deviation above and below the mean — this tells us we should consider ability scores between 9.6 and 15.1 typical.
It is worth noting that this method is a variation on the approach in earlier editions: roll 3d6. As shown below, it typically generates ability scores between 7.5 and 13.5, with a mean of 10.5. This is why 10 is sometimes quoted as the average ability score of a regular person: it is slightly below the expected score of an adventurer, who must be better than average to survive.
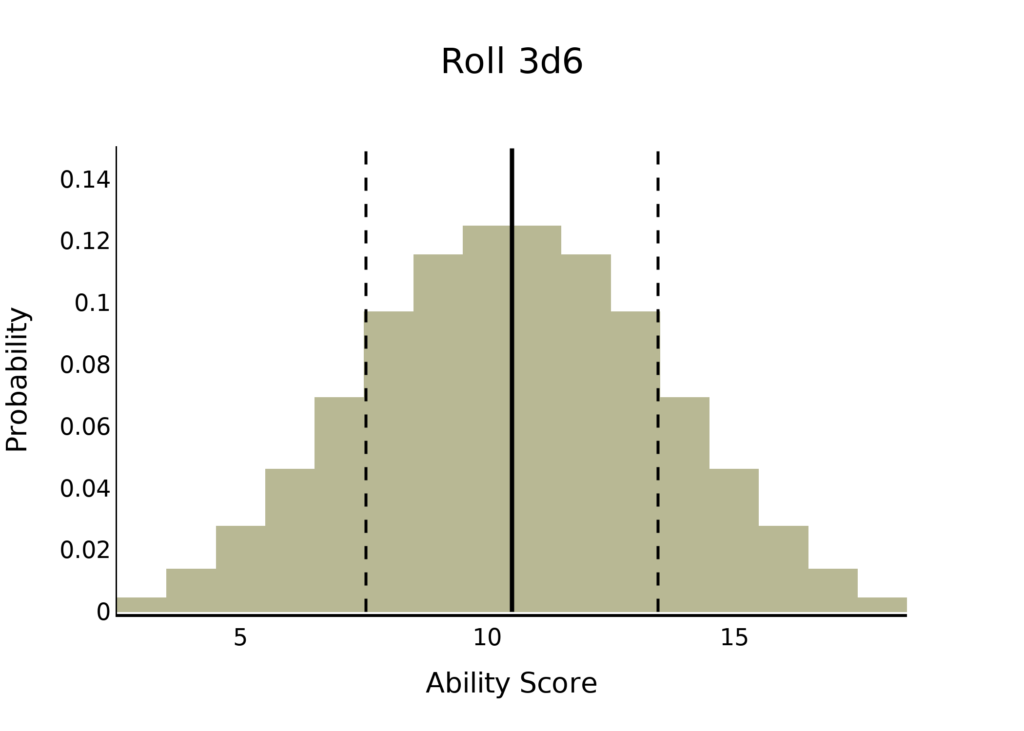
The motivation for using the updated method is visible here. Dropping the lowest roll makes the lower end of the distribution less likely, and the upper end more common. No one wants to play a character who rolls a three for all six ability scores, so the shifted probability makes this less likely. However, it does not solve this issue: hopelessly under-powered and overpowered characters are still possible. More importantly, it can lead to a gulf in power levels of characters in a party. One player’s character may be significantly better than everyone else due to random variation.
The Standard Array
Rather than rolling, players can assign ability scores from a fixed list: [15, 14, 13, 12, 10, 8]. For the sake of comparison, the mean is 12.0, and one standard deviation either way gives a range of 9.6 to 14.4. This fits the dream distribution: after adding racial bonuses, there could be a 17, two 14, and a 12, 10, and 8 we do not care about. Wizards of the Coast seem to endorse my conclusion there. The range and distribution are slightly worse than roll 4d6, suggesting that the gamble of rolling is encouraged, and the price for avoiding risk is worse ability scores that you might have otherwise.
Point Buy
The final option in the PHB is the most complex. It is also the only one that explicitly requires DM permission. Point Buy works by giving each player a pool of 27 points with which to purchase different ability scores. An 8 is free, and the highest available score is a 15, costing 9 points.
Unlike rolling, this method does not result in the same distributions for each ability score. This method is stateful: the available points to spend on one ability score depend on what was spent before. The rolling methods were stateless: the generation of each score is independent of what came before.
Unfortunately, this is significantly harder to analyse. As later ability scores depend on earlier ones, the distribution will be different not only for each ability score, but for each possible set of previously selected ability scores. As they are interrelated, we cannot meaningfully compare individual ability scores — only full sets of 6. This is much harder to visualise, but we shall try nonetheless.
Selecting 6 ability scores from 8 options allows in 866 possible sets of ability scores — that 262,144. To keep things manageable, we can reduce this to the set of unique sets that we can afford for 27 points. That leaves 1197. Note that these are unordered sets, so [15,15,15,8,8,8] and [8,8,8,15,15,15] are considered the same. Of these 1197, some are strictly worse than others, like [9,9,9,9,9,9] and [10,10,10,10,10,10]. Removing those leaves just 65.
As these sets of ability scores have internal connections, we cannot look at the total distribution of the whole set. Instead, we must look at the distributions of each of the 65 groups. We can do that with a box plot with far too much data:
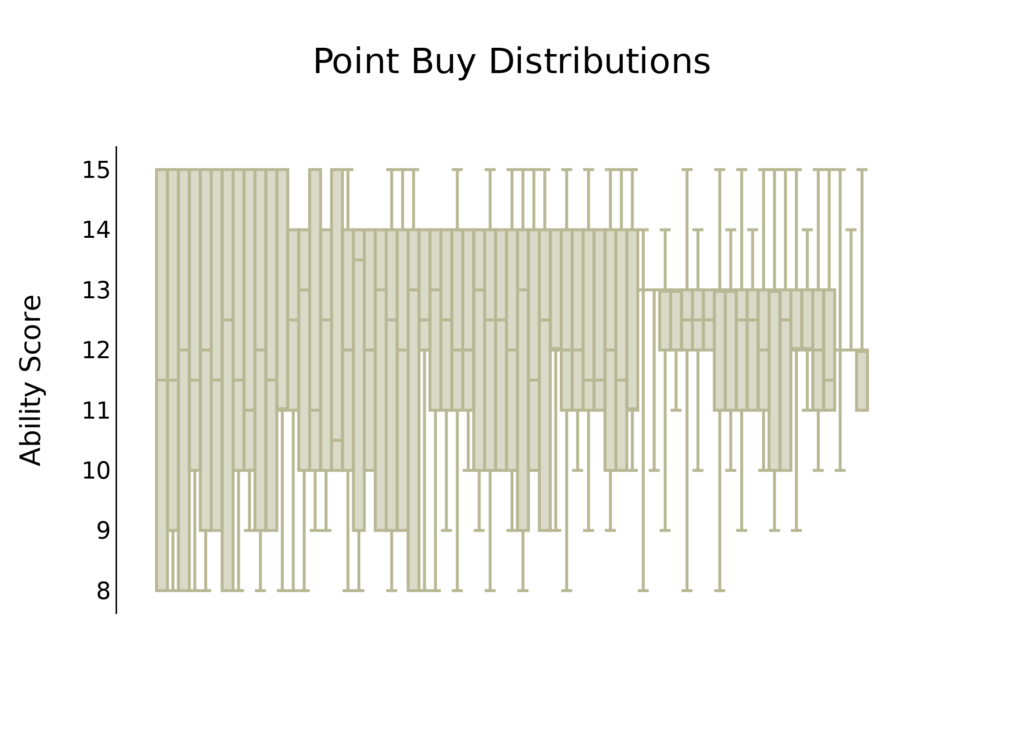
Point buy seems to deliver exactly what it offers. You can choose to generate some high scores and some low, compromise so they are all middling, or go somewhere in between. The means of each set range from 11.5 to 12.5, with a mean mean of 12.1. The mean standard deviation is
The means of these ability score distributions range from 11.5 to 12.5, with a mean mean of 12.1. The mean standard deviation is 2.0, suggesting point buy tends to give ability scores on a lower range.
Comparisons
These methods all produce roughly similar results. The means and standard deviations are all quite similar: about 12.2 and 2.5. The less random methods make 3 high values and 5 low impossible, suggesting they are primarily intended to prevent the lower numbers.
The simplest method is the standard array. It will reliably produce a functioning character, is is free from the risks of chance. However, it is not particularly fun — there is nothing exciting about picking numbers from a list.
Rolling dice is fun — if you do not enjoy rolling dice, you have picked the wrong game. However, there is a risk of creating an unfair character who is either too weak or too strong. More subtly, these methods tend to produce very similar results. The smoothing effect of adding multiple rolls means characters with a 12 for every ability are more likely than characters with a mix of strengths and weaknesses, and as discussed under the dream array, having some strengths is more important than not having weaknesses, so a well-rounded set of ability scores is somewhat undesirable.
Point Buy is complicated. This can be particularly intimidating for new players, who do not yet know the value of different abilities or ability scores, so are ill-suites to judge the costs and benefits of different options. I consider this a significant flaw. By raising the entry bar, we make the game less accessible. However, it does offer players the most reliable way to sculpt their characters.
Ability Scores Done Differently
The official mechanisms are clearly all usable, although they have some drawbacks. These limitations are sufficiently well-known that several alternatives have been proposed.
Roll In Order
This is not an alternative way of generating ability scores, but assigning them. Rather than allocating scores to their choice of ability, players assign the scores they generate to Strength, Dexterity, Constitution, Wisdom, Intelligence, and Charisma in that order. Proponents argue that this encourages players to try more original characters and different builds from what they have used before. While this may be true, it is not something I would encourage.
Different players enjoy different parts of the game. Some like the power and complexity of spellcasting; others like the strategy of combat and the thrill of the kill; still others want to live out the lives of particular archetypes or heroes; and others just want something simple they can use as an excuse to join the game and hang out with their friends. As a DM, I would rather enable my players to do what they enjoy than compel them to play the game in a different way.
Group Generation
This is a compromise between randomly generating ability scores and ensuring everyone in the group gets a fair set. Although there are variations on the theme, the most common approach is for all players to roll ability scores by some method, then for the group to pick one set for everyone to use. I find this approach unsatisfying, as it does not actually address the underlying issue. The only result is that ability scores will generally be higher than they would be otherwise.
Dice Variations
There are ways to vary the dice rolling. These achieve a similar result to switching from 3d6 to 4d6 drop lowest: they try to keep some random element while removing low scores. I am addressing them heuristically, as these methods encompass many sub-variations.
The first is to roll additional scores. Players could generate seven ability scores and keep six, or two sets of six and keep one, or three sets of three and so on. I have the same objections here as to group generation.
The second is to give the players more control over the dice pool. They could have a pool 24d6, and allocate them into six piles (like six sets of 4d6, or three of 3d6 and three of 5d6), roll them, and sum the greatest three in each to generate ability scores. This could be combined with Roll In Order so that players get random scores, but have some influence over which ability scores will likely be higher. Alternatively, players could roll 3d6 to generate a score, then keep rolling more from their pool to try and raise it, before moving on to the next one. This forces them to choose between trying to raise an ability score now, and risking rolling a lower one later.
The dice pool variants have merit. They are fairly intuitive (roll more for better), allow a degree of control over the produced distributions, and still hinge on dice rolls. I will refrain from adding further figures, but the results of this method should follow from the 3d6 and 4d6 histograms.
The Deck of Many Ability Scores
Point buy solves the problem of randomly generated scores unfairly empowering, or worse dis-empowering, players. In fact, this also makes the DM’s life harder, as it makes any general method of estimating the party’s abilities unreliable. Point Buy’s solution made use of state so that each generated ability score had an impact on the next, however it is very complex, and requires a thorough understanding of mechanical maths to use effectively. Dice pools take some of this state, but are ultimately still subject to the same risks of randomness. The solution to all of this is to find a new mechanism for generating random numbers that is both simple and stateful.
I first found the suggestion of using cards on a forum several years ago. I have seen it resurface occasionally since, but do not know the original source, so sadly cannot give credit.
The methods works as follows: the DM creates a deck of 12 cards. Each player draws six pairs, and uses the sums of each to generate ability scores, before shuffling them back into the deck for the next player. This is both random and simple, and we can show it has the stateful properties we want.
As the deck always contains the same cards, and all cards are drawn, the sum of all ability scores (and therefore mean) will always be the same. We can stack the deck so that it is impossible not to get a dream distribution with at least the scores we want players to have. Finally, as cards that have already been drawn are no longer available, we have state. A player who draws a low card may be briefly frustrated, but they also know all other ability scores will be better, while a player who draws lots of good cards should have a growing sense of foreboding.
I will not visualise the distributions this produces. Every ordering of cards will produce a new set, and unlike Point Buy we cannot ignore duplicates, as they affect the probability distribution. With 12 cards, there are 479,001,600 possible orderings. As such, we will have to rely on analysis.
Make the Deck
First, we need to design the deck. There is space to tailor this to your campaign’s needs, so I will explain my reasoning. To match the means of the PHB methods, the deck’s total should be about 73-74. I want there to be at most two scores under 10, so no more than four cards under five. I settled for [3,3,4,4], as I felt drawing a 2 would be too disheartening, but drawing a three would be disappointing but not particularly consequential. This means the lowest possible score is 6, and the lowest pairs are 6 and 8 or 7 and 7. I wanted the highest score to feel powerful, so I chose 17, facilitated by adding an 8 and a 9 to the deck. Drawing 8 and 9 together will be rare enough to be exciting, but the state mechanism means the character will end up with other weaknesses. Capping things at 9 also spares me assigning meaning to face cards, which makes it easier to explain.
Filling in the gaps required some tinkering — I graphed a few thousand random samples and their standard deviations, and eventually settled on [9,8,8,8,8,7,6,6,4,4,3,3]. Using four eights means this can be done with a normal deck of cards, and will feel top-heavy. The ability score set with the lowest maximum is [12,11,12,12,14,13]. With racial bonuses this only just falls short of our desired goal, so should still make for a viable character. The set with both the highest and lowest possible scores is [17,16,15,12,8,6], which makes for a powerful character with significant vulnerabilities.
In most cases, this method will lead to interesting distributions. Unlike 4d6, which tends towards the mean, the state mechanism at play here pushes scores towards extremes. Every above average score will necessitate a below average score to balance it.
As a variation, you can allow players a swap. Once they have drawn all cards, they can switch any two. This lets them tailor their scores to their liking without introduce major complexity. Choosing not to performing a swap will not cause a player to fall behind.
What I Do
My preferred method is the card deck. I do not allow swaps in order to make it as simple as possible, however I do make this step one of character creation. This means players who want to build around a particular idea can pick a race to fill in the gaps. Others might be inspired by the distribution they get, and change their character plans to lean into it more heavily.
Go Forth
That covers all the (sane) ways I am aware of for generating ability scores. Hopefully you can see that deciding the method to use here is not without consequences. Not only will it determine how capable your PCs are and how balanced the party feels, but it will impact the on-boarding experience of new players. Do you have a favorite method, or have other factors that influence your decision? If so, drop a comment!